The problem quickly becomes very complex if the usual parallel and series resistor equations are used. It can be done, but there are easier methods. It is quite simple if symmetry is invoked.
Suppose a current of 3 A flows through the supply leads. Since the cube has a 3-fold symmetry about rotations through the axis connecting the input and output leads, each of the 3 resistors attached to the input corner carries the same current: 1 A. Likewise each of the 6 resistors one edge away from the input (and output) must carry 0.5 A and each of the 3 resistors next to the output lead must carry 1 A. Similarly, the voltage at each of the nodes (corners) one edge (resistor) away from the input must all be the same, and likewise for the voltage at the nodes one edge away from the output lead.
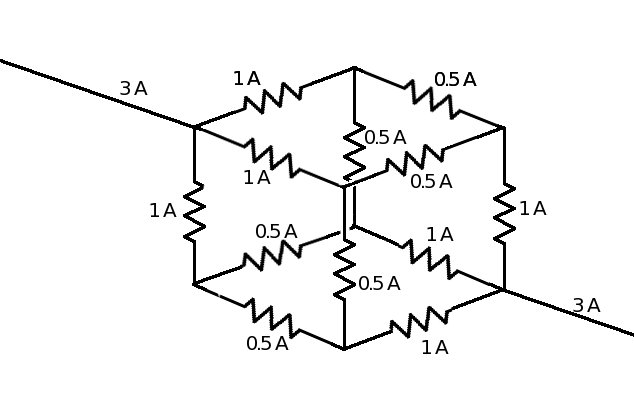
Therefore the total voltage across the assembly is 1 V + 0.5 V + 1 V = 2.5 V . Using Ohm’s Law R=V/I, the resistance is 2.5 V / 3 A = 0.833 Ohms.
